정렬 알고리즘

1. 선택 정렬 (Selection Sort)

선택정렬

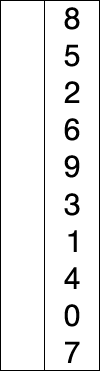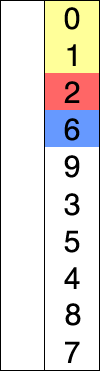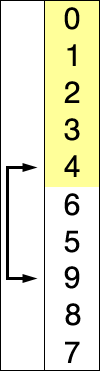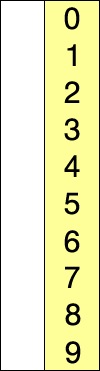
가장 기초적인 정렬 알고리즘이다.

알고리즘
1. 배열의 맨 앞부터 순회한다.
2. 각 인덱스부터 최솟값을 찾는다.
3. 인덱스의 값과 최솟값의 위치를 변경한다.
시간복잡도
- Best Case : O(n^2)
  
  정렬이 되어있어도 최솟값을 확인해야 하기 때문에 O(n^2)이다.
- Worst Case : O(n^2)

구현

const selectionSort = (arr) => {
  let minIndex;
  for (let i = 0; i < arr.length - 1; i++) {
    minIndex = i;
    for (let j = i + 1; j < arr.length; j++) {
      if (arr[minIndex] > arr[j]) {
        minIndex = j;
      }
    }
    if (i != minIndex) {
      const temp = arr[minIndex];
      arr[minIndex] = arr[i];
      arr[i] = temp;
    }
  }
  return arr;
};

2. 삽입 정렬 (Insertion Sort)

삽입정렬

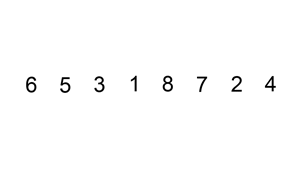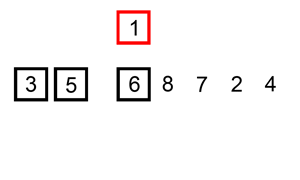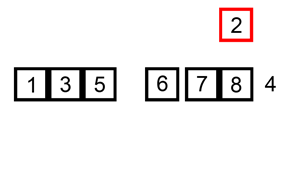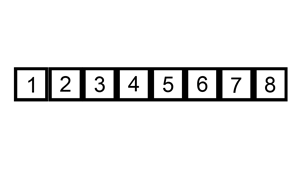
알고리즘
1. 두 번째 원소부터 순회한다.
2. 현지 위치의 값을 key로 두고, key의 앞(j) 부터 역순으로 탐색한다.
  
  key보다 j의 값이 작으면 현재 위치의 값을 오른쪽(j+1)으로 한칸 옮겨준다.
  
  key보다 원소가 크거나 같아지면 그 위치가 key가 들어갈 위치이다.
시간복잡도
- Best Case : O(n)
  
  모든 원소가 정렬되어있을 경우 key당 1번씩만 비교한다.
- Worst Case : O(n^2)
  
  key당 key-1번의 비교를 수행해야 되므로
  
  1 + 2 + … + n-2 + n-1= n(n-1)/2이다.

구현

const insertionSort = (arr) => {
  for (let i = 1; i < arr.length; i++) {
    const key = arr[i];
    let j;
    for (j = i - 1; j >= 0; j--) {
      if (key >= arr[j]) {
        break;
      }
      arr[j + 1] = arr[j];
    }
    arr[j + 1] = key;
  }
};

3. 버블 정렬 (Bubble Sort)

버블정렬

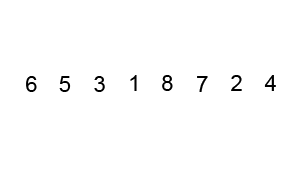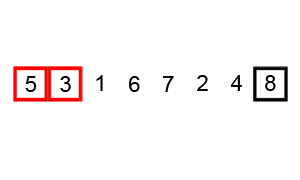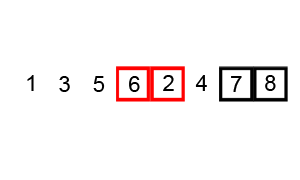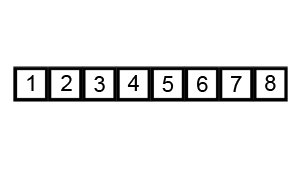
최댓값이 거품처럼 위로 올라온다고 해서 붙여진 이름이다.

알고리즘
1. 처음 인덱스부터 마지막 인덱스까지 인접한 2개의 원소를 비교하며 큰 값을 뒤로 옮긴다.
2. 1번의 결과로 가장 큰 값이 맨 뒤로 옮겨진다.
3. 1번의 과정에서 마지막 인덱스를 한개씩 줄여 큰값을 계속 뒤로 옮겨준다.
시간복잡도
- Best Case : O(n^2)
  
  정렬되어 있어도 앞뒤 값을 모두 비교해줘야한다.
- Worst Case : O(n^2)

구현

const bubbleSort = (arr) => {
  for (let i = 0; i < arr.length - 1; i++) {
    for (let j = 0; j < arr.length - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        const temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
      }
    }
  }
};

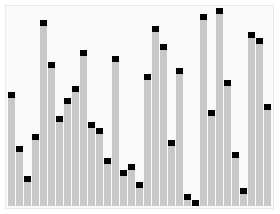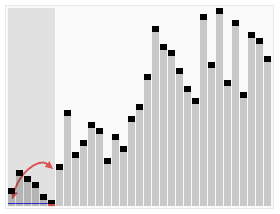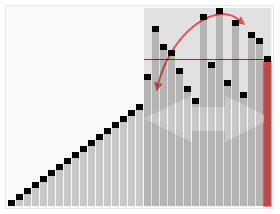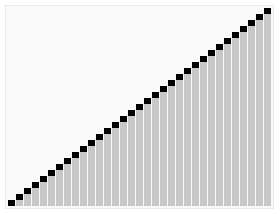
4. 퀵 정렬

기준값을 중심으로 부분집합을 나눠 분할하여 정복하는 알고리즘이다.

Divide & Conquer 의 대표적인 알고리즘 중 하나이다.

퀵정렬

알고리즘
1. 기준값 pivot을 적절한 값으로 정한다.
2. pivot보다 작은 값을 왼쪽, 큰 값을 오른쪽으로 모은다.
3. 나눈 배열에 대해 위 1,2번을 반복한다.
시간복잡도
- Best Case : O(nlogn)
  
  배열을 반씩 나눠서 비교하므로 logn번 반복하고 각 횟수당 비교의 총 합이 배열의 길이 n이기 때문에 시간복잡도는 nlogn이다.
- Worst Case : O(n^2)
  
  배열이 정렬되있을 경우 pivot은 가장 큰 값이거나 가장 작은값이다.
  
  이 때 pivot에 의한 분할이 n번 일어나며 배열을 n번 비교하므로 O(n^2)이다.

구현

공간목잡도를 고려한 방식

const partition = (arr, begin, end) => {
  // 첫 번째 값으로 pivot 설정
  let pivot = arr[begin];
  // pivot 다음 부터 시작
  let left = begin + 1;
  // 범위의 오른쪽부터 시작
  let right = end;

  // 범위가 교차되지 않을 때 까지
  while (left <= right) {
    // 왼쪽부터 pivot보다 크거나 같은 값을 찾는다.
    while (arr[left] < pivot) {
      left++;
    }
    // 오른쪽부터 pivot보다 작은거나 같은 값을 찾는다.
    while (arr[right] > pivot) {
      right--;
    }
    // 범위가 교차되지 않는다면, pivot보다 큰 값과 작은 값을 swap
    if (left <= right) {
      const temp = arr[left];
      arr[left] = arr[right];
      arr[right] = temp;
      left++;
      right--;
    }
  }
  // pivot이 들어갈 위치에 pivot 삽입
  const temp = arr[right];
  arr[right] = arr[begin];
  arr[begin] = temp;
  return right;
};
const quickSort = (arr, begin, end) => {
  if (begin < end) {
    const pivotIndex = partition(arr, begin, end);
    quickSort(arr, begin, pivotIndex - 1);
    quickSort(arr, pivotIndex + 1, end);
  }
};

공간복잡도를 고려하지 않은 방식

const quickSort = (arr) => {
  if (arr.length <= 1) return arr;
  const left = [];
  const right = [];
  let pivot = arr[0];
  for (let i = 1; i < arr.length; i++) {
    if (arr[i] <= pivot) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }
  const sortedLeft = quickSort(left);
  const sortedRight = quickSort(right);
  sortedLeft.push(pivot);
  sortedLeft.concat(sortedRight);
};

5. 합병 정렬 (Merge sort)

Divide & Conquer 의 대표적인 알고리즘 중 하나이다.

데이터의 배열 상태에 영향을 크게 받지 않는다.

합병정렬

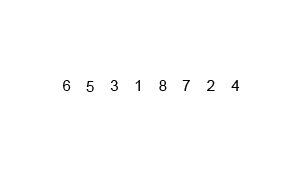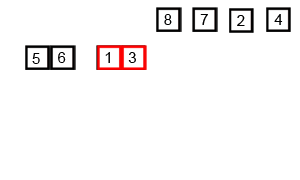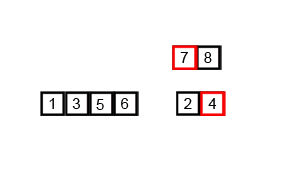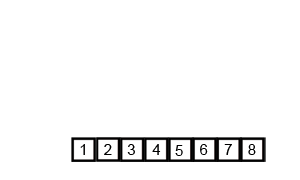
알고리즘
1. 각 배열의 길이가 1이 될 때 까지 2개의 부분 배열로 분할한다.
2. 2개의 리스트를 각각 처음부터 하나씩 비교하며 작은 값을 새로운 배열에 옮긴다.
3. 2의 연산 후 2개의 배열 중 값이 남아있는 배열의 값들을 새로운 배열에 옮긴다.
4. 새로운 배열의 정렬된 값들을 원본 배열에 반영한다.
시간복잡도
- Best Case : O(nlogn)
- Worst Case : O(nlogn)
  
  항상 배열을 절반으로 나누기 때문에 logn번 반복하고 각 횟수당 비교 연산의 총 합은 n번이기 때문에 시간복잡도는 nlogn이다.

구현

const merge = (arr, left, mid, right) => {
  // 왼쪽부터
  let l = left;
  // 중간 +1부터
  let r = mid + 1;
  // 정렬된 값 임시 저장 자료구조
  const tempArr = [];

  // 왼쪽 또는 오른쪽의 값을 다 쓸때 까지
  while (l <= mid && r <= right) {
    //왼쪽이 작으면 왼쪽꺼 넣어줌
    if (arr[l] < arr[r]) {
      tempArr.push(arr[l]);
      l++;
      //오른쪽께 작으면 오른쪽꺼 넣어줌
    } else {
      tempArr.push(arr[r]);
      r++;
    }
  }
  //한쪽 배열에 남아있는 값들을 다 넣어줌
  if (l > mid) {
    for (let i = r; i <= right; i++) {
      tempArr.push(arr[i]);
    }
  } else {
    for (let i = l; i <= mid; i++) {
      tempArr.push(arr[i]);
    }
  }
  // temp에 있는 배열 arr로 옮겨줌 (정렬된 배열 반영)
  for (let i = left; i <= right; i++) {
    arr[i] = tempArr[i - left];
  }
};

const mergeSort = (arr, left, right) => {
  if (left < right) {
    const mid = Math.floor((left + right) / 2);
    mergeSort(arr, left, mid);
    mergeSort(arr, mid + 1, right);
    merge(arr, left, mid, right);
  }
};

해당 자료의 모든 이미지 파일의 출처는 위키피디아 입니다.